Transformations 3D: Quaternions Duals
Représentations de transformations rigides à l’aide des dual quaternions
Motivations
Les angles d’Euler et les matrices de transformation 4x4. Les angles d’Euler, bien qu’intuitifs, souffrent du phénomène de verrouillage de gimbal, une singularité rendant certaines rotations impossibles. En contraste, les quaternions offrent une représentation sans ambiguïté et sans singularité des rotations, ce qui les rend particulièrement adaptés aux calculs nécessitant des interpolations fluides et des rotations continues. Les dual quaternions, quant à eux, étendent ces avantages en intégrant translations et rotations en une seule structure compacte, simplifiant ainsi les calculs de transformation et les rendant plus robustes et efficaces.
Afin de mieux comprendre l’intérêt de cette nouvelle complexité par rapport aux plus instinctifs angles d’Euler, rappelons que les angles d’Euler sont construits en choisissant successivement plusieurs axes de rotation. Pour une base \(B_0 (x_0,y_0,z_0)\) on peut choisir de tourner autour de \(x_0, y_0\) ou \(z_0\). La base \(B_1\) ainsi formée par cette rotation, on doit de nouveau choisir un nouvel axe de rotation non confondu avec le précédent. Finalement on obtient bien trois angles qui caractérisent une rotation dans l’espace mais selon la séquence choisie, ce triplet ne décrira pas la même situation comme illustré ci-dessous, les deux rotations on pour coordonnées (90°,90°,90°) mais sont pourtant bien différentes.
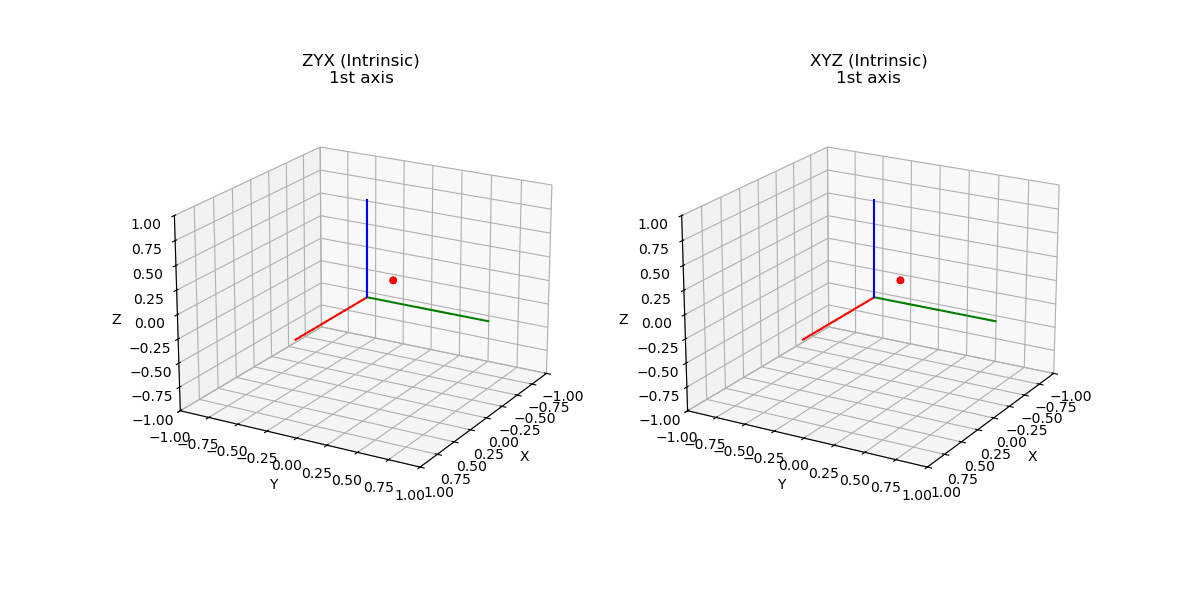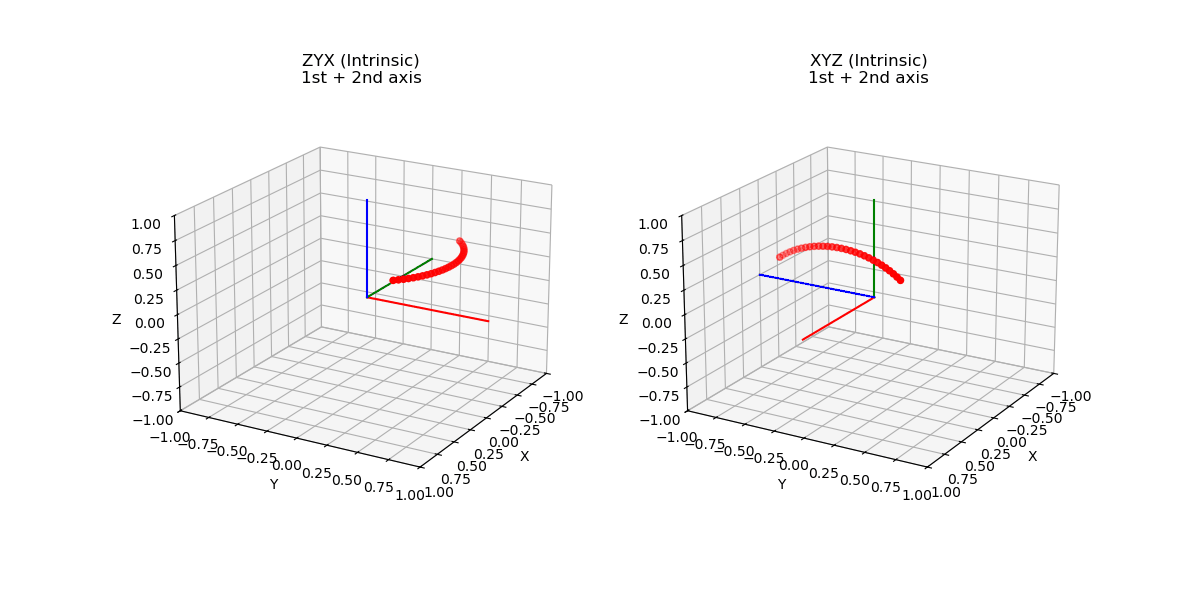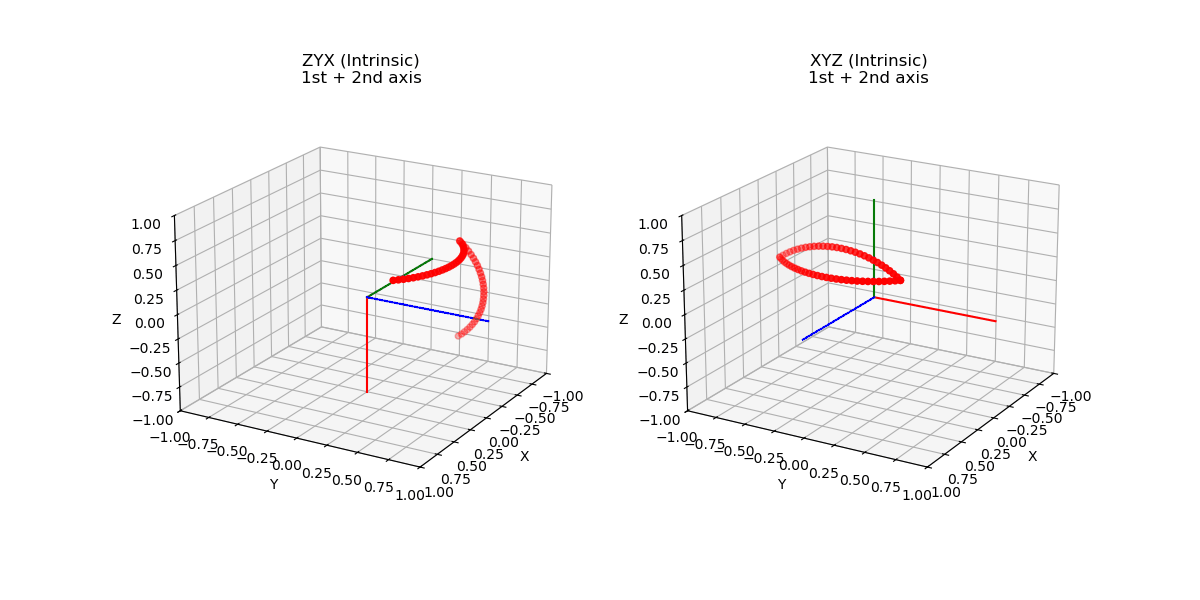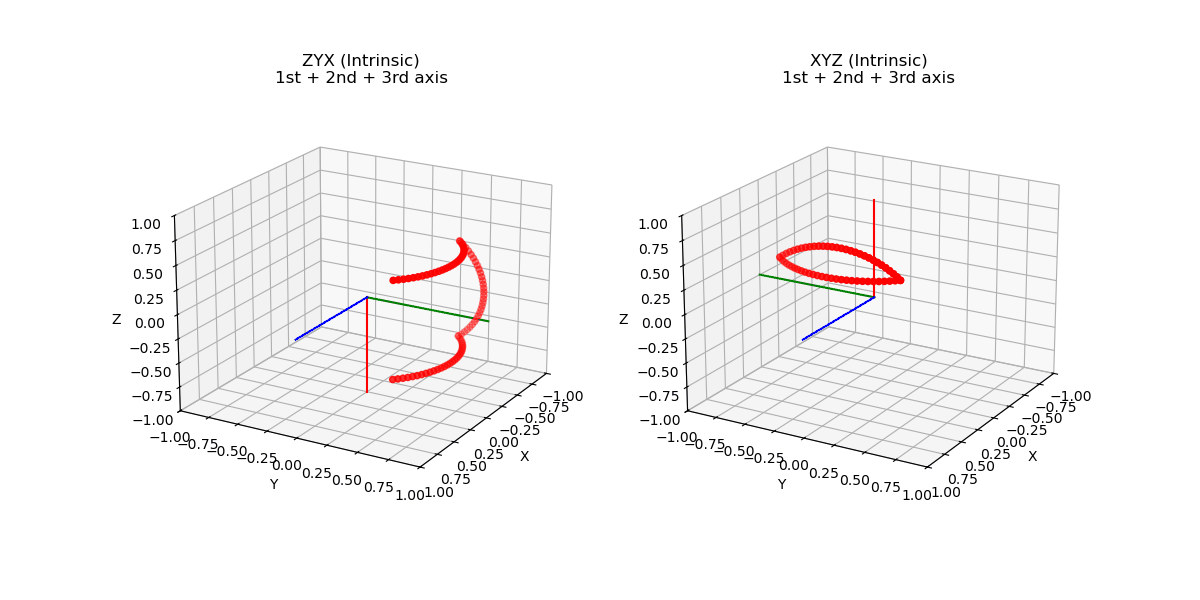
Par ailleurs, dans l’exemple précédent on a construit la rotation en choisissant de tourner autour de l’axe de la base nouvellement créee, on
parle de rotation intrinsèque. Nous aurions très bien pu décider de définir la rotation non pas en tournant autour d’un axe de la nouvelle base
mais en tournant autour d’un axe de la base initiale ! On parle de rotation extrinsèque, ajoutant encore plus de caractère arbitraire à ce type de représentation. On illustre ci-dessous la différence entre une rotation intrinsèque et extrinsèque.
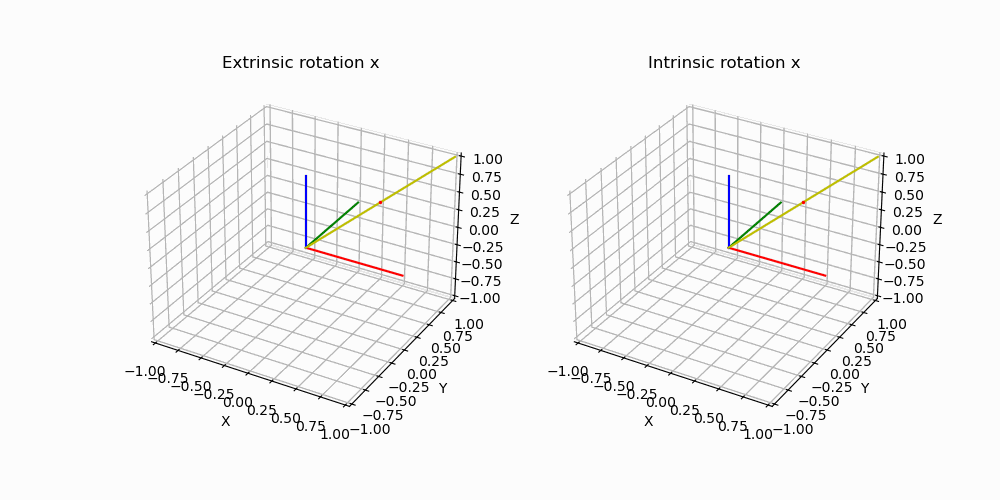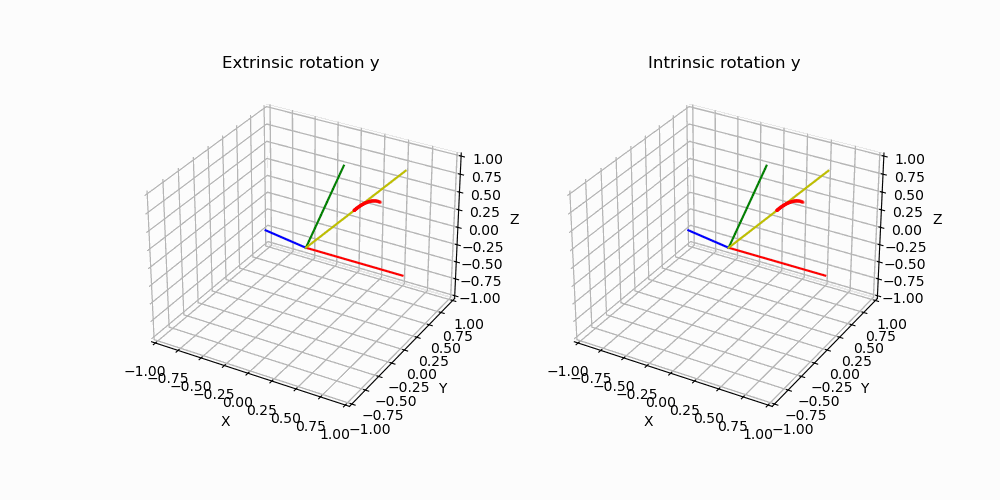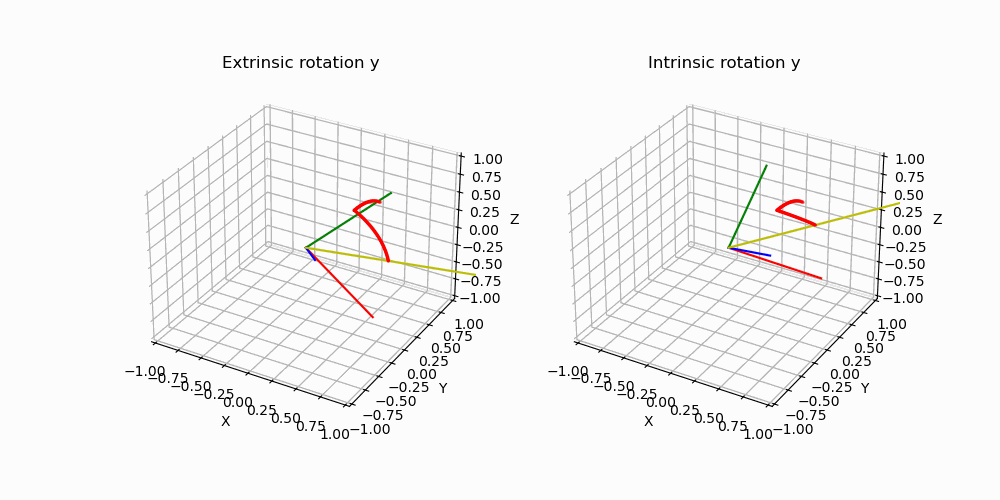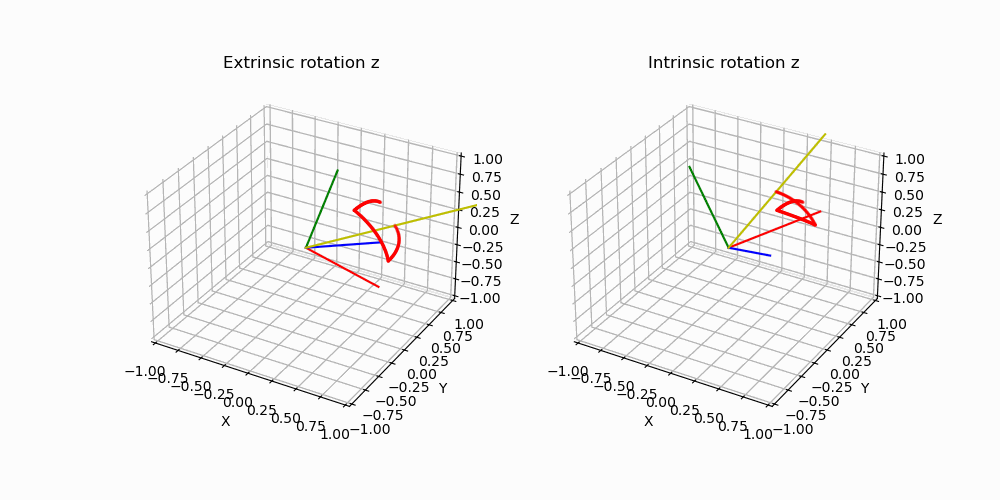
De cette ambiguitée des représentations on comprend l’intérêt d’une représentation sans ambiguitée et plus compacte pour représenter des
transformations 3D. On cherchera à travers cette article à démistifier l’objet quaternion et dual quaternion, leur application pour décrire
des transformations ou problèmes physique et par ailleurs présenter la librairie YAQLE (Yet Another Quaternion Library for Embedded) qui a été développée pour traiter ce genre de problème
en embarqué.
Il n’existe pas à l’heure où j’ai commencé ce projet, une librairie C++ adaptée pour du calcul sur cible embarquée ET permettant de convertir explicitement les différentes combinaisons d’angles d’Euler (Intrinsèque/Extrinsèque compris).
Quaternions
Définitions
Un quaternion peut être vu comme une extension des nombres complexes à quatre dimensions mais dont la multiplication n’est pas commutative:
\[q = q_0 + q_1i + q_2j + q_3k\]où \(q_0\) est la partie réelle et \(q_1i + q_2j + q_3k\) représente la partie imaginaire. On notera parfois sous la forme vectorielle \(q = (q_0, q_1, q_2, q_3)\)
Par définition, \(i,j,k\) des nombres complexes tels que:
\[i^2 \equiv j^2 \equiv k^2 \equiv ijk \equiv -1\]Parties réelles et imaginaires
De façon analogue aux nombres imaginaires classiques on définit respectivement une partie réelle et imaginaire d’un quaternion \(q = (q_0,q_1,q_2,q_3)\)
\[\Re{(q)} \equiv (q_0,0,0,0)\] \[\Im{(q)} \equiv (0,q_1,q_2,q_3)\]Conjugués
On note \(q^\star\) le conjugué de \(q\) et par définition:
\[q^\star = (q_0,-q_1,-q_2,-q_3)\]Norme
On étend naturellement la notion de norme euclidienne aux quaternions. La définition de la norme est très importante car dans l’ensemble des quaternions, seuls les quaternions unitaires ont un intérêt pour nos applications.
\[\lVert q \rVert = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2}\]Propriétés
Non Commutativité
La multiplication de quaternion n’est pas commutative par définition. Donc si l’on reprend la dernière égalité de la définition des quaternions \(ijk \equiv -1\)
On en déduit directement:
\(ij = k\) et \(ji = -k\)
\(jk = i\) et \(kj = -i\)
\(ki = j\) et \(ik = -j\)
Si l’on fait le parallèle avec les produits vectoriel où dans une base directe, \(x \wedge y = z\) et \(y \wedge x = -z\).
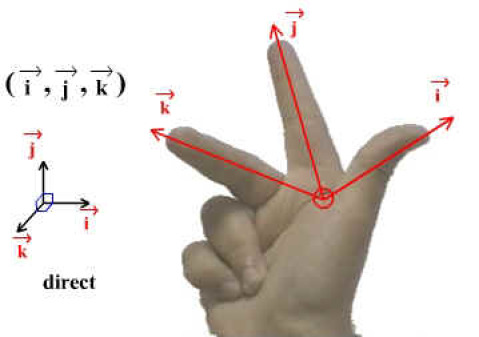
Addition de quaternion
Soient \(Q_a\) et \(Q_b\) deux quaternions alors
\[Q_a + Q_b = (Q_{a0} + Q_{b0}, Q_{a1} + Q_{b1}, Q_{a2} + Q_{b2}, Q_{a3} + Q_{b3})\]Multiplication de quaternion
A l’aide des propriétés évoquées précédement, le développement d’un produit entre deux quaternions arbitraires est laborieux mais se fait facilement. On peut démontrer que le produit de deux quaternions \(Q_a\) et \(Q_b\) se condence de la façon suivante:
\[Q_aQ_b = (Q_{a0}Q_{b0} - \Im{(Q_a)} \cdot \Im{(Q_b)} , Q_{a0} \Im{(Q_b)} + Q_{b0} \Im{(Q_a)} + \Im{(Q_a)} \wedge \Im{(Q_b)})\]où \(\Im{(Q_a)} \cdot \Im{(Q_b)}\) représente le produit scalaire des parties imaginaires de \(Q_a\) et \(Q_b\).
Rotations
Un quaternion unitaire (c’est-à-dire de norme 1) peut être utilisé pour représenter une rotation 3D sans ambiguïté :
\[v'=q.v.q^\star\]où \(v'\) est le nouveau vecteur 3D une fois transformé, \(q\) un quaternion unitaire représentant une rotation et \(q^\star\) son conjugué.
Contrairement aux matrices de rotation 3×3, les quaternions :
- Ne souffrent pas de singularités,
- S’interpolent facilement (via slerp),
- Sont plus compacts (4 paramètres au lieu de 9).
Dans YAQLE, un quaternion est encapsulé dans la classe Quat, qui expose une interface minimaliste et optimisée pour les systèmes embarqués (basée sur ETL – Embedded Template Library) Quelques fonctionnalités notables :
- Opérations algébriques : addition, produit, conjugué, inversion, normalisation ;
- Conversions explicites : vers et depuis les angles d’Euler, avec choix de séquence (XYZ, ZYX, etc.) et de convention (intrinsèque ou extrinsèque) ;
- Rotation de vecteurs : Vector3D rotate(Vector3D const &v) ;
- Interpolation : lerp et slerp pour transitions douces entre orientations.
using namespace yaqle;
Quat q = fromEuler({90, 45, 0}, Quat::ZYX, true);
Vector3D v = {1, 0, 0};
Vector3D v_rot = rotate(q, v);
Cette représentation offre déjà une base solide pour décrire les orientations dans l’espace. Mais dès qu’on cherche à décrire non seulement l’orientation, mais aussi la position, les quaternions seuls ne suffisent plus. C’est là qu’interviennent les quaternions duaux.
Quaternions Duaux
Définitions
Les dual quaternions combinent rotation et translation au sein d’une seule structure mathématique :
\[\hat{q} = q_r + \epsilon q_d\]où :
- \(q_r\) est le quaternion unitaire représantant la rotation
- \(q_d = \frac{1}{2}tq_r\) encode la translation \(t\) un quaternion imaginaire pur \((0,x ,y, z)\).
- \(\epsilon\) est un nouveau type de nombre complexe appelé nombre dual tel que \(\epsilon^2 = 0\) avec \(\epsilon \neq 0\)
On a donc en quelque sorte élevé les nombres complexes à un degré supplémentaire en introduisant un nouveau nombre \(\epsilon\) avec ses nouvelles propriétés. On comprend dès lors que les définitions usuelles de conjugué, norme deviennent plus délicates puisqu’on peut imaginer un conjugué au sens dual comme au sens ‘usuel’.
Ainsi, une transformation rigide (rotation + translation) peut être appliquée directement à un point ou à un autre dual quaternion sans passer par des matrices homogènes.
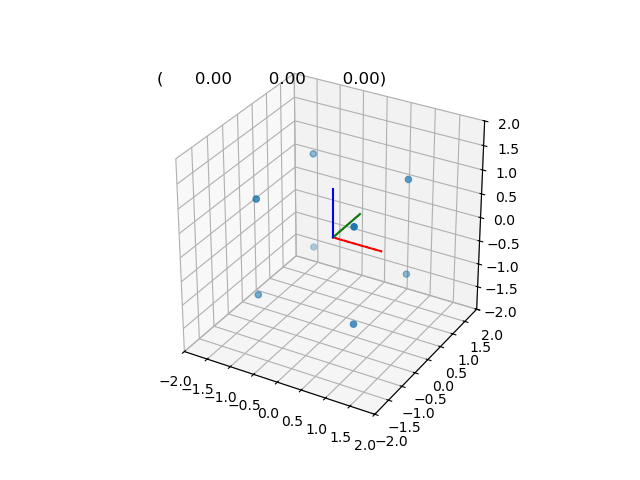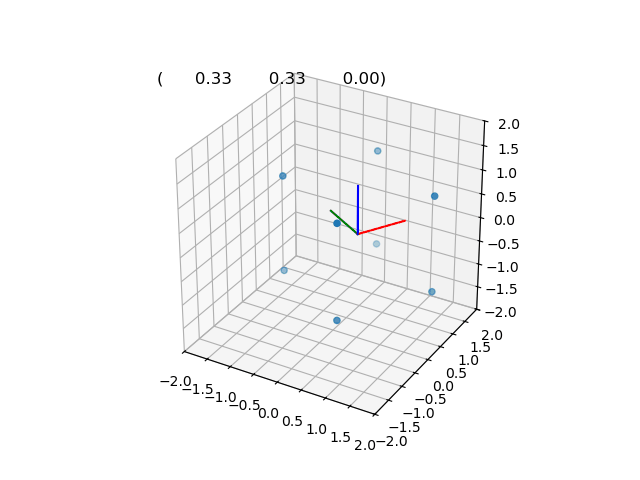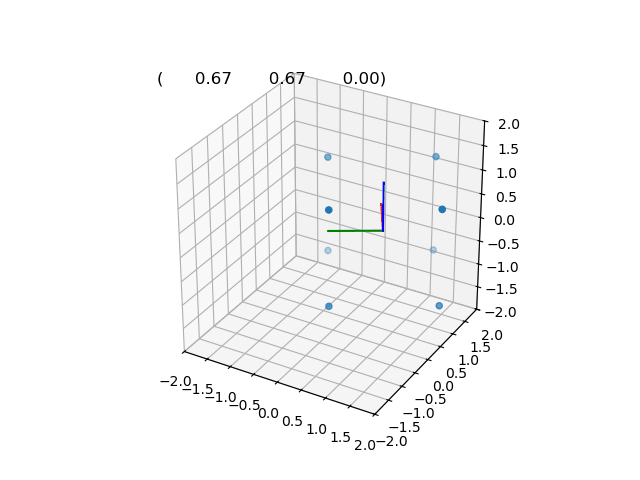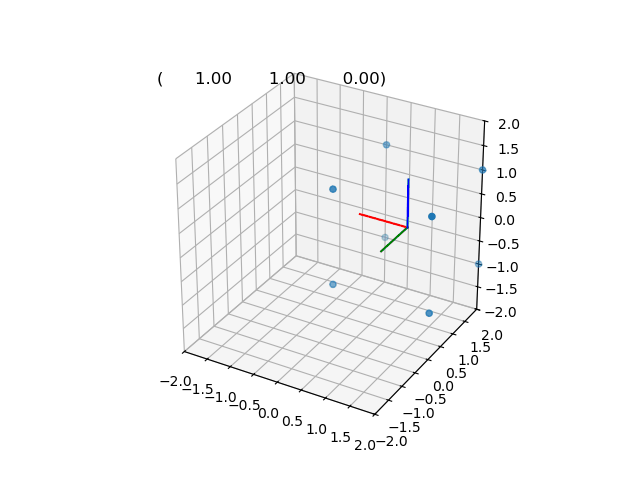
\[\hat{p'} = \hat{dq}.\hat{p}.\hat{dq}^\star\]Interpolation de la position 0 à la position +pi (1,1,0)
DQ0 = rigidTransform(unitQuat(1, 0, 0, 0), 0, 0, 0); // Pose initiale
DQ1 = rigidTransform(unitQuat(M_PI_2, 0, 0, 1), 1, 1, 0); // Pose finale
file = ofstream("dual_slerp.txt");
for (float t = 0; t < 1; t += 0.01)
{
DQuat dq = slerp(DQ0, DQ1, t); // Interpolation des poses
dq.writeToFile(file);
}